Medios de enlace

Los medios de enlace son las vías por las cuales se comunican los datos desde el transmisor hasta el receptor.

Lo que se transmiten son ondas electromagnéticas o pulsos de luz.

Clasificación:

Los medios de enlace se clasifican en medios guíados, (en los cuales los datos se conducen a través de cables o alambres), y en medios no guíados o «inalámbricos» en los cuales el medio de transmisión es el aire.

Dentro de los medios de transmisión no guiados tenemos las antenas.

Dentro de los medios de transmisión guiados tenemos a las guías de onda, a las fibras ópticas y a las líneas de transmisión (que incluyen a los cables coaxiles, a los cables bifilares, a las lineas planares microstrip y a las lineas planares stripline).

En los siguientes posts estudiaremos cada uno de ellos.

Primer parcial 17/04/2019 Problema 4

Enunciado

Determinar:

A) La constante de fase (5 puntos)

B) La longitud de onda (10 puntos)

C) El campo H (15 puntos)

Resolución:

Primer parcial 17/04/2019 Problema 3

Enunciado

Determinar:

A) La constante de atenuación (5 puntos)

B) La constante de fase (5 puntos)

C) La longitud de onda (5 puntos)

D) La profundidad de penetración (5 puntos)

Resolución:

Primer parcial 17/04/2019 Problema 2

Enunciado

Hallar la distribución del potencial electrostático V(r) de un cable coaxial que tiene radio del conductor interno a y radio del conductor externo b. Con dieléctrico aire (sin carga libre), el radio interno conectado a una batería Vo y el conductor externo conectado a tierra (25 puntos).

Resolución

Esquema del problema: Tenemos una cable coaxil con radios internos a y b conectado a un potencial Vo en el radio interno y un potencial cero en el conductor externo.

Primer parcial 17/04/2019 Problema 1

Enunciado:

Dos placas metálicas paralelas, de extensión infinitas, están separadas una distancia d y conectadas a una tensión constante Vo y tierra como lo indica la figura. Entre ambas existe una distribución de cargas de manera que ρ=q/z³.

Se pide:

A) Hallar la expresión del potencial entre las placas V(z) (expresando las condiciones de borde, y verificando la expresión encontrada para cada condición) (10 puntos)

B) Encontrar el campo eléctrico entre las placas (10 puntos)

C) Dibujar el campo eléctrico encontrado en B. (5 puntos)

Resolución

Adaptación de la linea de transmisión

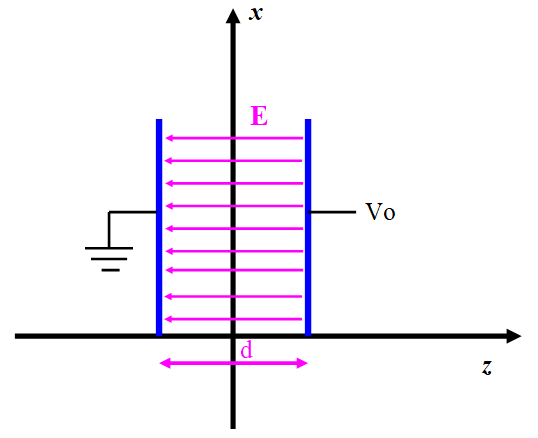
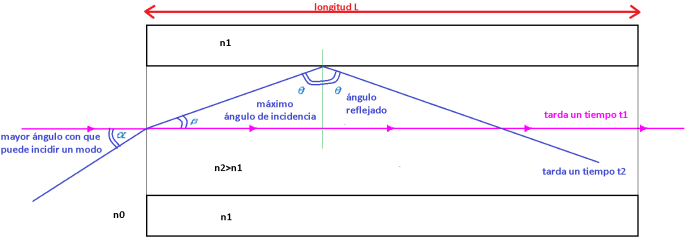
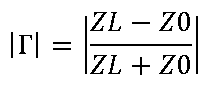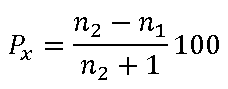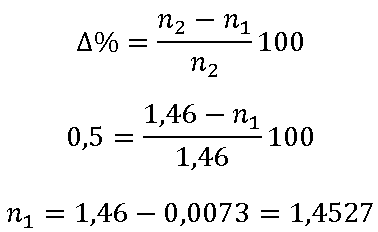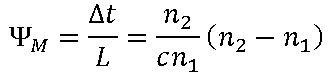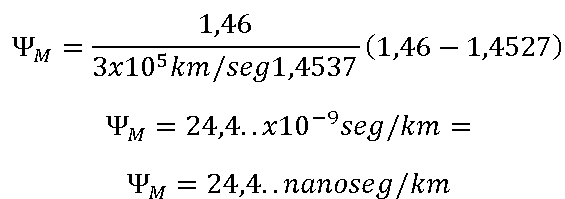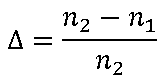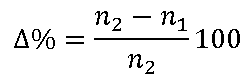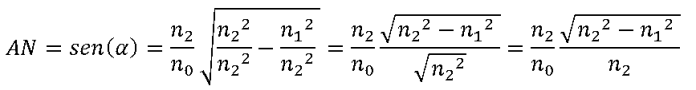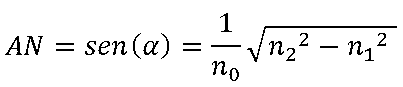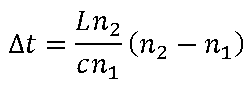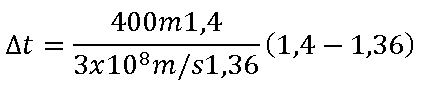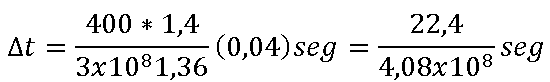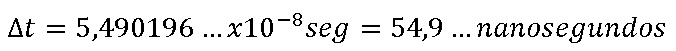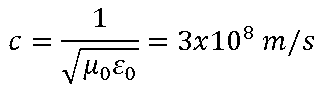Queremos que a la carga le llegue la máxima potencia posible.

La energía que entrega el generador a la carga es máxima cuando ZL (la impedancia de la carga) y Zg (la impedancia del generador) son impedancias conjugadas, es decir que tienen la misma parte real pero parte imaginaria opuesta.

Pero además queremos evitar que parte de la potencia que llega a la carga vuelva reflejada hacia la entrada.

Si conseguimos que el generador entregue la máxima potencia que puede entregarle a una carga, las pérdidas por atenuación aún no las podemos evitar. Pero si podemos lograr que la potencia que llegue a la carga no vuelva reflejada hacia la entrada.

Esto lo conseguimos solo cuando el coeficiente de reflexión es cero. Como el módulo del coeficiente de reflexión es

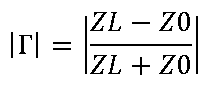
solo se hace cero cuando la impedancia característica de la linea Z0 es igual a la impedancia de la carga ZL.

Métodos para adaptar impedancias

En general hay dos métodos que se utilizan para adaptar impedancias. Uno es con un transformador de cuarto de onda,y otro es con un Stub.

Para saber como adaptar con ambos de ellos usamos el diagrama de Smith. Para usar el diagrama de Smith podemos pensar como que en el diagrama estamos «yendo» desde la carga hacia el generador, y siempre que estamos «pasando» por una de las lineas tenemos que estar normalizados respecto a su impedancia.

Adaptar con un Transformador de cuarto de onda

El transformador de cuarto de onda es una linea de longitud λ/4 (un cuarto de la longitud de onda) de impedancia característica Zt. Se coloca en serie con la linea de transmisión, a una distancia d de la carga.

En general los datos suelen ser la impedancia característica de la linea que queremos adaptar (Z0), la impedancia de la carga (ZL) y la frecuencia a la que vamos a trabajar (f), mientras que las incógnitas suelen ser la impedancia característica del transformador (Zt) y la distancia de la carga a la que lo queremos colocar (d).

Pasos para adaptar con el diagrama de Smith

Ingresamos la impedancia de la carga (ZL) normalizada respecto a la impedancia de la linea (Z0), en el diagrama de Smith

Ingresar ZL/Z0

Entonces me muevo por una circunferencia de radio ZL/Z0 (y centro en el centro del diagrama) en sentido horario (ya que voy desde la carga hacia el generador) hasta cortar el eje horizontal, que corresponde con impedancias resistivas puras.

Me muevo hasta cortar el eje horizontal, encuentro Zr/Z0

Cuando las impedancias son resistivas puras (Zr), adapto con una linea de longitud de onda λ/4 de cual conozco su valor de impedancia característica (Zt) que es la raíz cuadrada de la impedancia de la linea que quiero adaptar (Z0) multiplicada por Zr

Zt = raíz de {Zr * Z0}

Allí es donde puedo colocar el transformador de cuarto de onda, entonces desde la carga me moví una longitud d, que es la distancia a la que tengo que colocar el transformador. En el diagrama corresponde al arco de circunferencia entre ZL/Z0 y Zr/Z0, que se mide desde la circunferencia más externa del diagrama. Ese valor es la cantidad de λ.

Conociendo la relación entre la longitud de onda λ, la velocidad de la luz c, y la frecuencia f a la que trabajamos, puedo despejar λ

c=λf  ==>  λ=c/f

Si tengo el valor de λ puedo expresar d en metros, centímetros, etc.

d = arco de la circunferencia más externa, entre ZL/Z0 y Zr/Z0

Luego desnormalizo respecto a Z0 y normalizo respecto a Zt. Para ello multiplico por Z0 y divido por Zr. Esto corresponde a pasar de un tramo de la linea con impedancia Z0 (la que quiero adaptar) a un tramo de linea del transformador, que tiene impedancia Zt.

desnormalizo respecto a Z0 y normalizo respecto a Zt

Z0*(Zr/Z0) / Zt

Luego me muevo una longitud λ/4 lo cual es como moverme 180º en el diagrama

me muevo λ/4

Llego a otro tramo de la linea que quiero adaptar. Entonces desnormalizo respecto a Zt y normalizo respecto a Z0

desnormalizo respecto a Zt y normalizo respecto a Z0

Zt*(Zr/Zt) / Z0

Debería obtener un 1

Adaptación con un Stub

El stub es una linea de transmisión de impedancia característica Z0 (igual a la impedancia característica de la linea de transmisión que queremos adaptar), que tiene una longitud ls (longitud del stub) y que se coloca en paralelo a una distancia d de la carga.

En general los datos suelen ser Z0, ZL y la frecuencia f, mientras que las incógnitas suelen ser la longitud del stub (ls) y la distancia a la que queremos colocarlo (d).

El stub se coloca en paralelo por lo cual se trabaja con admitancias. Para que este adaptado hay que conseguir que Yab sea igual a 1.

Pasos para adaptar con el diagrama de Smith

Comenzamos ingresando ZL normalizado respecto a Z0 en el diagrama de Smith.

Ingresar ZL/Z0

Luego trazamos una circunferencia cuyo centro sea el punto del centro del diagrama de Smith, y que pase por ZL/Z0.

YL/Z0 va a estar diametralmente opuesto a ZL/Z0, es decir que hay que trazar una recta que pase por el centro y por ZL/Z0 y el lugar donde corte a la circunferencia del otro lado es YL/Z0.

Encontrar YL/Z0 diametralmente opuesta

Luego por esa misma circunferencia nos movemos en sentido horario (comenzamos en la carga y nos movemos hacia el generador), hasta cortar la circunferencia que se corresponde a g=1 (estamos buscando encontrar Yab = G+jB que sea igual a 1).

Encontrar Yab en la circunferencia con g=1

Si miramos la circunferencia más externa del diagrama de Smith, encontramos que distancia d nos movimos desde la carga para llegar al transformador, que esta expresada en función de λ

Encontrar d, el arco de la circunferencia externa desde YL/Z0 hasta Yab

Sabiendo que la longitud de onda es la velocidad de la luz sobre la frecuencia, podemos encontrar la longitud de onda y dejar expresada d en las unidades de longitud cm, m, etc

c=λf  ==>  λ=c/f

Luego queremos que Yab sea igual a 1, entonces queremos cancelar su parte imaginaria. Yab = 1 +jB, entonces buscamos el valor «-jB» que corresponde al opuesto d e la parte imaginaria de Yab.

Buscar el valor que anula la parte imaginaria de Yab

Si el Stub está en corto circuito entonces tiene una impedancia cero es decir una admitancia infinita. Entonces nos movemos desde el extremo derecho del diagrama, siempre en sentido horario (hacia el generador), hasta llegar al valor que anula la parte reactiva de Yab. Nos movimos un arco de circunferencia ls (la longitud del stub). Si el stub estuviera en circuito abierto entonces correspondería a una impedancia infinita es decir a una admitancia cero, entonces nos moveríamos desde el extremo izquierdo del diagrama, siempre en sentido horario, hasta el valor que anule la parte imaginaria de Yab (es decir, una longitud ls)

Desde el c.ab. o el corto. del stub, nos movimos un arco de circunferencia ls

¿Cómo calcular atenuaciones sin pasar de mW a dbm?

Si no paso a dbm, en vez de sumar y restar potencias tengo que trabajar con logaritmos, entonces

Atenuación = -10 log ( P2 / P1 )

Por ejemplo, en el problema sobre la reflexión de Fresnell

P1 era 20 W

La atenuación era de 6 dbm

Entonces P2 en watt lo podríamos haber hallado despejandolo de

6 dbm = -10 log ( P2 / 20 W )

De donde

0,2512.. = P2 / 20 W    ==>   P2 = 5023,77.. mW

Y obtenemos el mismo valor

También lo podríamos haber usado en la segunda parte, luego de obtener que P2′ era de 1098,95.. mW

6 dbm = -10 log ( P1′ / P2′ )

6 dbm = -10 log ( P1′ / 1098,95.. mW )

0,2512.. = P1′ / 1098,95.. mW   ==>   P1′ = 276,04.. mW

Y también obtenemos el mismo valor

Notar que siempre la atenuación es menos 10 veces el logaritmo en base 10 de la potencia que llega sobre la potencia que sale.

 

Problema sobre potencia en la fibra óptica

Un enlace de fibra óptica de 15 km de longitud utiliza una fibra óptica cuya atenuación es de 1,5 db/km. Los tramos de fibra óptica que se conectan entre sí tienen una longitud de 1 km. Siendo las pérdidas del conector 0,8 dbm y la de los empalmes 0,3 dbm. Determinar el valor mínimo de la potencia óptica media de entrada que se debe entregar al enlace de manera que la potencia óptica media a su salida sea de 0,3 μW.

Resolución manera 1

La potencia P1 (en dbm) que se debe entregar en la entrada tiene que ser por lo menos la potencia que me piden a la salida P2 (en dbm) más los dbm que se atenúan debido a transmitir esa potencia por la fibra óptica.

P1 (dbm) – P2 (dbm) = Atenuación total

Pasamos la potencia P2 a dbm

P2 (dbm) = 10 log (0,3 μW /1mW)      ==>      P2 = -35,23..dbm

La atenuación en la fibra óptica es la suma de las atenuaciones debidas a sus distintas componentes, entonces

Atenuación total = Ate(conectores) + Ate(empalmes) + Ate(longitud fibra)

Hay 2 conectores que atenúan 0,8 dbm cada uno. Hay empalmes cada 1 km y la fibra óptica tiene una longitud de 15 km, por lo cual hay 14 empalmes y atenúan 0,3 dbm cada uno. La longitud de la fibra es 15 km y atenúa 1,5 dmb cada kilómetro, entonces

Atenuación total = 2*0,8 dbm + 14*0,3 dbm + 15 km * 1,5 dbm/km

Atenuación total = 38,13 dbm

Despejando P1

P1 (dbm) – (-35,23..dbm) = 38,13 dbm

P1 = 2,9012.. dbm

Pasando a mW (no lo pide, así que este paso es opcional)

2,9012… dbm = 10 log ( P1(mW) /1mW )

P1 = 1,95.. mW

Resolución manera 2

La atenuación en la fibra óptica es menos diez veces el logaritmo de la potencia de salida sobre la potencia de entrada, es decir

Atenuación = -10log(P2/P1)

Reemplazando el valor de la atenuación y de la potencia de salida P2 queda

38,13 dB = -10 log (0,3µW / P1)

Pasando el -10 dividiendo queda

-3,813 = log (0,3µW / P1)

Aplicando 10 a la x a ambos lados de la igualdad queda

1,5381546403030347517730819469765e-4‬ = 0,3µW / P1

Despejando P1

P1 = 0,3µW / 1,5381546403030347517730819469765e-4

P1 = 1,95.. mW

Obtenemos el mismo resultado que de la manera 1 (que pasando todo a dbm).

Problema sobre la frecuencia normalizada V

Dada una fibra óptica multimodo, con el diámetro del núcleo de 60 micrones y una diferencia relativa entre los índices de refracción de 1,5%, que opera con λ = 0,85 micrones.

Si el índice de refracción del núcleo es 1,48 calcular el número de modos que se propagan.

Resolución

La diferencia relativa entre los índices de refracción es 1,5%, entonces

Δ% = (n2-n1)/n2 * 100 = 1,5%

(clickea el siguiente enlace Diferencia relativa de índices de refracción si quieres repasar el tema!)

De donde conozco el índice de refracción del núcleo n2 = 1,48 y puedo despejar a n1

(1,48-n1)/1,48 * 100 = 1,5       ==>      n1 = 1,4578

Me piden calcular el número de modos que se propagan en la fibra óptica sabiendo que es multimodo. Podría checkear que la frecuencia normalizada de la fibra óptica es mayor que 2,405 (lo cual se cumple en todas las fibras multimodo)

V = 2πr * raízde {n2² – n1²} / λ

(clickea el siguiente enlace Frecuencia normalizada de la fibra óptica si quieres repasar el tema!)

Como el diámetro es de 60 micrones, el radio es de 30 micrones, entonces

V = 2π*30 micrones * raízde {1,48² – 1,4578²} / 0,85 micrones

V = 60π * raízde {0,06521916} / 0,85

V = 56,63…

Como V>2,405, efectivamente es una fibra multimodo.

Encontrando la cantidad de modos

La cantidad de modos es la frecuencia normalizada V al cuadrado sobre 2

cant de modos = V² / 2

 cant de modos = 56,63..² / 2

 cant de modos = 1603,65

Se propagan 1603 modos.

Problema de potencia en la fibra óptica

Un sistema que opera a una longitud de onda de 1,3 micrones (ventana óptica 2) usado para un enlace de fibra de 50 km requiere como mínimo 0,3 mW en el detector para su detección. Las pérdidas de la fibra óptica son 0,5 dbm/km. La fibra es empalmada cada 5 km y tiene 2 conectores de 1 dbm de pérdidas cada uno. Las pérdidas en los empalmes son de solo 0,2 db por empalme. Determinar la potencia mínima que debe ser inyectada a la fibra en mW y en dbm.

Resolución

Podemos calcular la atenuación total debida a todos los elementos de la fibra óptica.

At total = Ate (conectores) + Ate (empalmes) + Ate (longitud fibra)

Como la fibra tiene 50 km y se empalma cada 5 km, se necesitan 9 empalmes. Además la atenuación en la fibra es de 0,5dbm/km, y como su longitud es 50 km, la atenuación es de 0,5*50 dbm = 25 dbm. Luego

At total = 2*1dbm + 9*0,2dbm + 0,5dbm/km*50km

At total = 28,8 dbm

De la potencia P1 que sea emitida, necesito recibir al menos P2 = 0,3 mW en el detector. Paso P2 a dbm para trabajar con atenuaciones

P2 (dbm) = 10 log ( 0,3mW /1mW )

P2 = -5,228787..dbm

Luego, si sumo la potencia que quiero que llegue (P2) más la cantidad que si o si se va a atenuar (At total), obtengo la potencia mínima que necesito inyectar en la entrada (P1)

P1 (dbm) = P2 + atenuaciones

P1 = -5,228787.. dbm + 28,8 dbm = 23,57.. dbm

Nos piden dejar a P1 también expresado en mW

23,57.. dbm = 10 log ( P1(mW) / 1mW )

P1 = 227,57.. mW

Esa es  la potencia mínima que necesitamos que sea inyectada.

El dato sobre la longitud de onda no era necesario para resolver el problema.

Problema de potencia con Reflexión de Fresnell

Un enlace de fibra óptica aéreo se abre a 20 km del transmisor. Si el emisor envía una potencia luminosa de 20 watt. ¿Qué potencia regresa al mismo sabiendo que la atenuación de la fibra óptica es de 0,3 dbm x km y el índice de refracción del núcleo es n2 = 1,56?

Resolución

Atenuación

Parte de la potencia P1 que emite el transmisor es atenuada, por lo cual la potencia P2 que llega al receptor es menor que P1. Para ver cuánto vale P2, pasamos todo a dbm

De watt a dbm

P1 (dbm) = 10 log ( 20 W / 1mW ) = 10 log (20000 mW / 1mW)

P1 = 43,01..dbm

Luego, la potencia emitida (en dbm) menos la potencia que llega (P2 en dbm) es igual a la atenuación

P1 (dbm) – P2 (dbm) = Atenuación

Donde la atenuación de la fibra óptica es de 0,3 dbm por kilómetro, por lo que hay que multiplicarla por su longitud que es de 20 km, entonces hay una atenuación

Atenuación = 0,3 dbm/km * 20 km = 6 dbm

Luego despejamos el valor de P2

43,01.. – P2 (dbm) = 6 dbm

P2 = 37,01.. dbm

Reflexión

Para ver que parte de la potencia P2 se refleja hacia la entrada, usamos la ecuación

Como es un enlace aéreo, n1 es el índice de refracción del aire que es aproximadamente 1

Luego un 21,875 % de P2 (expresada en watt) se refleja hacia la entrada.

Pasando de dbm a watt

37,01.. dbm = 10 log ( P2(mW) /1mW )

P2 = 5023,77.. mW

Si llamamos P2′ a la potencia que vuelve, con una regla de 3

P2 = 5023,77..mW es el 100%

P2′ es el 21,875%

Luego P2′ = 5023,77..mW * 21,875 % / 100 % = 1098,95.. mW

Luego esta es la potencia que vuelve hacia la entrada.

Atenuación

La potencia que vuelve hacia la entrada vuelve a través de la fibra óptica por lo cual se atenúa. Si llamamos P1′ a la potencia que efectivamente llega a la entrada, si las potencias están en dbm la diferencia entre la potencia que sale y la que llega es debida a la atenuación que es de 0,3 dbm/km * 20 km = 6 dbm al igual que antes

P2′(dbm) – P1′(dbm) = Atenuación

Pasamos a dbm

P2′ (dbm) = 10 log ( 1098,95 mW / 1mW ) = 30,41..dbm

Despejamos P1′(dbm)

30,41..dbm – P1′(dbm) = 6 dbm

Luego la potencia que vuelve a la entrada es de 24,41.. dbm.

Si queremos dejarla expresada en watt

24,41 dbm = 10 log ( P1′ (mW) / 1mW )

P1′ = 276,04.. mW

Regresa una potencia de 276,04.. mW.

«Para calcular atenuaciones conviene trabajar en dbm. Para calcular la potencia que vuelve reflejada, trabajamos en unidades de watt»

Reflexión de Fresnell

Parte de la potencia que emite el transmisor, al llegar al receptor es reflejada, es decir que vuelve de nuevo hacia la entrada. La potencia que va a volver es un porcentaje de la potencia P2 que llego al receptor. Este porcentaje depende de los índices de refracción y es el siguiente

Porcentaje que de la potencia P2 que vuelve a la entrada

Problema sobre Dispersión modal

Una fibra multimodo de índice abrupto tiene un índice de refracción del núcleo n2 = 1,46 y una diferencia relativa de índices de refracción de 0,5 %. ¿Cuál será el ensanchamiento del pulso por unidad de longitud debido a la dispersión modal?

Resolución

Que la fibra sea «de índice abrupto» quiere decir que el cambio entre el índice de refracción en la parte interna de la fibra óptica (el núcleo) y el índice de refracción del revestimiento externo, no es gradual sino abrupto. Eso lo cumplen todas las fibras con las que venimos trabajando.

Tenemos el índice de refracción n2 y la diferencia relativa porcentual entre índices, entonces podemos despejar n1

Luego, nos piden el ensanchamiento del pulso por unidad de longitud. Es decir que nos piden la dispersión modal, ya que la dispersión modal mide cuántos nanosegundos se ensancha el pulso por kilómetro.

La dispersión modal surge de dividir el ensanchamiento del pulso que es Δt, por la longitud de la fibra óptica, de donde surge la siguiente ecuación

Reemplazo por los datos del problema n2 = 1,46, el valor de n1 hallado n1 = 1,4527 y el valor de la velocidad de la luz que es c = 3×10^8 m/s, pero en kilómetros sobre segundo porque la dispersión modal tiene unidades de nanosegundos sobre kilómetro

Luego la dispersión modal (ensanchamiento del pulso por unidad de longitud) es de 24,4 nanosegundos por kilómetro.

Diferencia relativa de índices de refracción

La diferencia relativa de los índices de refracción es el cociente entre la diferencia de los mismos y el más grande de los dos índices de refracción. Es decir que este número me dice que fracción de n2 es la diferencia entre los índices.

No solo analiza si los mismos son muy parecidos (para eso bastaba con ver la diferencia), sino también compara esta diferencia con el valor de los índices, por esto es que se le llama diferencia relativa.

¿Por qué no simplemente la diferencia?

No es lo mismo tener una diferencia de 0,1 si los índices son de magnitudes cercanas a 5 que si por ejemplo sus magnitudes son cercanas a 0,3.

La interpretación es que este número representa que fracción de n2 es la diferencia entre ambos índices

Para hallar la diferencia en relativa en porcentaje podemos hacer una regla de 3 simple

n2 es el 100 %

n2-n1 es (n2-n1)x100% / n2

Esto quiere decir que hay que multiplicar a la diferencia relativa por 100

Y este número representa que porcentaje de n2 es la diferencia de los índices

Por ejemplo si n1 = 1,274 y n2 = 1,3 la diferencia porcentual relativa entre los índices de refracción es de un 2% ya que n2 – n1 = 0,026 lo cual es un 2% de 1,3.

Longitud de la fibra óptica, problema 2

En un enlace de fibra óptica la salida del transmisor es P1 = -5 dbm y la potencia de llegada al receptor es P2 = -14 dbm. Si se utiliza una fibra cuya atenuación es 0,5 dbm por km, ¿Qué longitud debe tener el enlace si se usan 2 conectores y 5 empalmes? Atenuación del conector = 1 dbm. Atenuación del empalme = 0,2 dbm.

Resolución

La diferencia entre la potencia que entrega el transmisor y la potencia que recibe el receptor, es igual a la atenuación de todos los componentes de la fibra óptica

P1 (dbm) – P2 (dbm) = Atenuación total

Esta atenuación es la suma de la atenuación en los 5 empalmes, de la atenuación en los dos conectores, y de la atenuación a lo largo de la longitud L de la fibra

Entonces

P1 (dbm) – P2 (dbm) = 2x Ate(conector) + 5x Ate(empalme) + Ate(fibra)

Reemplazamos los valores de las atenuaciones de cada componente y las potencias P1 y P2

-5 dbm – (-14dbm) = 2x 1dbm + 5x 0,2dbm + Ate(fibra)

La atenuación de la fibra es de 0,5 dbm por kilometro. Para saber la atenuación en toda su longitud hay que multiplicar por la cantidad de kilómetros de la fibra, es decir por su longitud L en kilómetros

Entonces la atenuación en toda su longitud es L * 0,5 dbm/km

Reemplazando

-5 dbm – (-14dbm) = 2x 1dbm + 5x 0,2dbm + L * 0,5 dbm/km

Los dbm se cancelan porque están en todos los términos

-5 – (-14) = 2x 1 + 5x 0,2 + L * 0,5/km

9 = 2 + 1 + L * 0,5/km

L = 12 km

Luego, la longitud de la fibra óptica es de 12 kilómetros.

Longitud de la fibra óptica, problema 1

La potencia óptica entregada por una fuente a un enlace de fibra óptica es de 1,5 miliwatt siendo la atenuación de la fibra óptica 0,5 dbm por kilómetro. Determinar la longitud máxima del enlace que se podría establecer utilizando dicha fibra si el máximo valor de potencia óptica media que hay que entregar al foto detector es de 2 microwatt.

Resolución

El transmisor entrega P1 = 1,5 mW de potencia pero el receptor necesita recibir P2 = 2μW. De allí podemos despejar la atenuación máxima que puede haber en la fibra óptica.

A pesar de que nos dan las potencias en watt conviene pasarlas a dbm ya que la atenuación total es igual a la diferencia entre las potencias P1 y P2 en dbm

Pasando las potencias a dbm

P1 (dbm) = 10 log ( 1,5mW/1mW ) = 10 log (1,5) = 1,7609.. dbm

P2 (dbm) = 10 log ( 2μW/1mW ) = 10 log (0,002) = -26,9897.. dbm

Relación entre la potencia del transmisor y del receptor

La atenuación es de 0,5 decibeles por cada kilometro de fibra óptica, entonces hay que multiplicarlo por la cantidad de kilometros que tenga (L es la longitud de la fibra en km)

P1 (dbm) – P2 (dbm) = Atenuación máxima = 0,5 dbm / km * L

Reemplazando P1 y P2

1,7609.. dbm – (-26,9897.. dbm) = 0,5 dbm / km * L

Despejando L

L = 28,7506…/0,5 km = 57,5.. km

Luego la longitud es de 57,5 kilómetros como máximo.

Potencia en la fibra óptica

Para trabajar con potencia en la fibra óptica muchas veces conviene pasar las potencias a unidades de dbm (es decir, decibeles de mili watt). La razón de ello es que entonces para hallar la potencia que se atenúa en la fibra óptica solo hay que restar la potencia en el transmisor menos la potencia en el receptor, mientras que al trabajar en watt la cuenta no es tan sencilla.

La diferencia entre P1 y P2 (entre el receptor y el transmisor), se debe a la atenuación en todos los elementos de la fibra óptica; en los conectores que en general son dos, en los empalmes si los hubiere, y en la longitud total de la fibra óptica.

De miliwatt a decibeles de miliwatt

Para pasar de mW a dbm hay que realizar la siguiente operación

P1 (dbm) = 10 log ( P1 / 1mW )

Donde log es el logaritmo en base 10

Frecuencia normalizada de la fibra óptica

Al parámetro V se lo conoce como frecuencia normalizada de la fibra óptica.

V es 2 pi veces el radio de la fibra óptica por la apertura numérica, sobre la longitud de onda, es decir

V = 2πr * raízde {n2² – n1²} / λ

V define el límite entre cuando una fibra es multimodo (la luz puede tener varias trayectorias al pasar por la fibra óptica) y cuando es monomodo (la luz solo puede tener una trayectoria al pasar por la fibra óptica)

V < 2,405    ==>   Fibra óptica Monomodo

V > 2,405    ==>   Fibra óptica Multimodo

El límite es cuando V = 2,405. Se define entonces la longitud de onda de corte

λcorte = 2πr * raízde{n2² – n1²} / 2,405

Que también define el límite entre fibras multimodo y fibras monomodo

V < λcorte   ==>   Fibra óptica Multimodo

V > λcorte   ==>   Fibra óptica Monomodo

Además, el número de modos (trayectorias) para la multimodo es

cant de modos = V² / 2

Problema de AN y el ángulo de asceptancia

Un rayo de luz viaja con una velocidad de 2,05×10^8 m/s en el núcleo de una fibra óptica. Si el ángulo crítico (límite en la interfase núcleo-revestimiento) es de 72º

Determinar cuánto valen

• La apertura numérica de la fibra óptica
• El ángulo de asceptancia  Ω

Resolución

La velocidad de la luz en el medio se puede hallar con esta ecuación

v=c/n2

Donde n2 es el índice de refracción del medio. En este caso la velocidad es dato, entonces podemos hallar n2 como

n2 = c/v    ==>   n2 = 3×10^8 m/s / 2,05×10^8 m/s   ==>   n2 = 3/2,05 = 1,4634..

La apertura numérica es el seno de alfa. Podemos hallarla usando la fórmula, pero como no tenemos el índice de refracción n1, intentamos otra manera

Usando la ley de Snell en el ángulo alfa

n0sen(∝) = n2sen(β)

Como el seno de beta es el coseno de θ

n0sen(∝) = n2cos(θ)

El índice de refracción del medio exterior, como no aclaran nada podemos suponer que es el índice de refracción del aire que vale aproximadamente 1. Además el ángulo θ es dato ya que es el ángulo «límite en la interfase núcleo-revestimiento», y es de 72º. Entonces

1sen(∝) = 1,4634..cos(72º)

Luego la apertura numérica es de

AN = sen(∝) = 1,4634..cos(72º)

Aproximadamente 0,4522.

Ángulo de susceptancia Ω

Los rayos que pueden incidir son los que forman un ángulo menor que alfa con el eje central de la fibra óptica. Todos ellos están dentro de un cono de base circular.

El ángulo de susceptancia Ω es el ángulo entre las paredes del cono que es dos veces el ángulo alfa.

 

En el problema conocemos la apertura numérica es decir el seno de alfa

Entonces el ángulo de susceptancia es

Ω = 2∝ = 2arcoseno(AN) = 53,77…º 

Apertura numérica

La apertura numérica es el seno del mayor ángulo con que puede incidir un modo en la fibra óptica, en el siguiente diagrama es el seno del ángulo alfa, es decir que se corresponde con el modo de máximo ángulo de incidencia al medio con n1.

Queremos despejar al seno de alfa en función de los parámetros n0, n1 y n2.

Despeje de la apertura numérica

Aplicando la ley de Snell en el ángulo alfa

sen(∝)n0=sen(β)n2

Despejando la apertura numérica AN

AN = sen(∝) = sen(β)n2 / n0

Además se cumple que el seno de beta es igual al coseno de tita, entonces

AN = sen(∝) = cos(θ)n2 / n0

Como θ es el ángulo crítico de la reflexión interna, la ley de snell para θ queda

sen(θ)n2=sen(90º)n1

De donde podemos despejar al seno de θ

sen(θ) = n1/n2

Pero en la ecuación de la apertura numérica aparece el seno de θ y no el coseno. Entonces usamos la siguiente igualdad

cos²(θ)+sen²(θ)=1

Y despejamos el coseno de θ en función del seno de θ, de donde

cos(θ) = raízde {1-sen²(θ)}

Reemplazando en la apertura numérica

AN = sen(∝) = raízde {1-sen²(θ)} n2 / n0

Reemplazando por lo que vale el seno θ

AN = sen(∝) = raízde {1 – (n1/n2)² } n2 / n0

Distribuyo el cuadrado en n1/n2, y escribo el «1» que está a la izquierda como n2 al cuadrado sobre n2 al cuadrado para hacer denominador común

El n2 que sale de la raíz se cancela con el que está afuera, luego la apertura numérica vale

 

 

Problema: Ver si los pulsos se solapan

Un tren de pulsos de luz es transmitido a lo largo de 400 metros de fibra óptica cuyos índices de refracción son n2=1,4 y n1=1,36. Estudiar los pulsos de salida para

• 10×10^6 pulsos por segundo (10 Mb/s)
• 20×10^6 pulsos por segundo (20 Mb/s)

*Suponer que el pulso de entrada tiene un ancho prácticamente igual a cero.

Resolución

Queremos ver que los pulsos lleguen, se ensanchen, pero que no se solapen. Para ver esto tenemos que conocer cual es su ancho (es decir, su duración) luego de pasar por la fibra.

Ensanchamiento del pulso

Para ver el ensanchamiento usamos la fórmula

Reemplazando por los datos del problema

Haciendo las cuentas

Luego el ensanchamiento del pulso es de

Como originalmente tenían un ancho despreciable, esta es la medida del ancho o duración final.

¿Qué información obtengo de los datos de los pulsos por segundo?

Si se cuantos pulsos vienen por segundo, por regla de 3 sé cuánto tiempo pasa entre que llega un pulso hasta que llega el próximo

Para el ítem a

vienen 10×10^6 pulsos                                                    en 1 segundo

                    1 pulso viene cada                         t = 1 pulso x 1 segundo / 10×10^6 pulsos

Los pulsos llegan cada 10^(-7) segundos, es decir cada 100 nanosegundos.

Para el ítem b

vienen 20×10^6 pulsos                                                    en 1 segundo

                    1 pulso viene cada                         t = 1 pulso x 1 segundo / 20×10^6 pulsos

Los pulsos llegan cada 0,5×10^(-7) segundos, es decir cada 50 nanosegundos.

Respuesta

Como los pulsos miden aproximadamente 55 nanosegundos de duración, si llegan cada 100 nanosegundos no se van a solapar, sin embargo si llegan cada 50 sí.

Entonces, para el ítem a no hay solapamiento, pero para el ítem b sí lo hay.

Conclusión

En conclusión a larga distancia no sirve la fibra multimodo, ya que la diferencia de tiempos entre el modo que tarda más y el modo que tarda menos Δt = t2 – t1 es proporcional a la longitud de la fibra óptica y el pulso se ensancha mucho por lo cual los pulsos se solapan.

==>    Para largas distancias, fibras monomodo  <==

Fibras ópticas

En las fibras ópticas se transmite información por medio de pulsos de luz. Al igual que en las guías de onda se intenta «guiar» a las ondas electromagnéticas a través de la fibra que suele ser de vidrio o plástico.

Alargamiento en la duración de los pulsos

La energía en la fibra óptica se propaga de distintos modos. Algunos siguen trayectorias rectas y otros ingresan con un cierto ángulo.

Para que no hayan perdidas, cuando el rayo intente pasar al medio con n1 no debe refractarse. Entonces el valor máximo que puede tomar el ángulo θ es aquel en que el ángulo refractado forma 90º con la normal.

Cumpliéndose la ley de snell, el seno del ángulo incidente (θ) por el índice de refracción de ese medio (n2) es igual al seno del ángulo refractado (seno de 90º) por el índice de refracción del medio al que incide el rayo (n1)

sen(θ)n2 = sen(90º)n1

De donde el seno del ángulo θ vale n1/n2

 

Fibra óptica

La diferencia entre el tiempo t2 del modo que tarda más y el tiempo t1 del modo que tarda menos, es el ensanchamiento del pulso.

Encontremos cuanto es el tiempo t1

La velocidad en el medio de índice de refracción n2 es c/n2

El modo que incide de forma horizontal recorre una distancia L en un tiempo t1, como velocidad es distancia recorrida sobre tiempo, el tiempo t1 lo podemos encontrar así

velocidad = L/t1        ==>     c/n2 = L/t1    ==>    t1 = Ln2/c

Encontremos cuanto es el tiempo t2

El modo que incide con el máximo ángulo de incidencia, recorre una distancia L’.

Esta distancia la podemos hallar con el seno del ángulo θ

El seno de un ángulo es cateto opuesto sobre hipotenusa, entonces el seno del ángulo θ es L sobre L’

sen(θ)=L/L’

Luego la velocidad c/n2 es la distancia recorrida L’ = L/sen(θ) sobre el tiempo transcurrido (t2)

c/n2 = { L/sen(θ) } / t2

De donde el tiempo transcurrido para este modo es

t2 = Ln2/csen(θ)

Reemplazando lo que vale el seno del ángulo θ

sen(θ)=n1/n2     ==>    t2 = Ln2 / c(n1/n2)    ==>    t2 = L(n2)² / cn1

Ensanchamiento del pulso

El ensanchamiento del pulso es la diferencia entre t1 y t2, entonces

Δt = t2 – t1

Δt = L(n2)² / cn1 – Ln2/c

Sacamos la longitud L por el índice n2 sobre la velocidad de la luz c, de factor común

Δt = Ln2/c {n2/n1 -1}

Haciendo denominador común

Δt = Ln2/c {n2/n1 -n1/n1}

El ensanchamiento del pulso es

Δt = Ln2/cn1 {n2 -n1}

Dispersión modal

La dispersión modal de una fibra óptica es esta diferencia de tiempos sobre la longitud de la fibra óptica, es decir

 

¿Cuantos modos transversales eléctricos pueden propagarse por la guía?

Una guía de onda rectangular con dimensiones a = 2,5 cm y b = 10 cm va a operar a una frecuencia de 15 GHz.

¿Cuántos medios transversales eléctricos pueden propagarse por la guía si el medio es el vacío?

Resolución

Conviene recordar que la velocidad de la luz la podemos hallar de esta forma

Vamos a trabajar a 15 GHz. Cada modo tiene una frecuencia de corte a partir de la cual empieza a propagarse. Encontremos la frecuencia de corte de cada modo para ver si van a propagarse a los 15 GHz

Modo transversal eléctrico 01

El modo TE 01 tiene valores m=0 y n=1. Para ver su frecuencia de corte reemplazamos los valores de m y n en la ecuación de la frecuencia de corte, y a mu y a epsilon (permeabilidad y permitividad del medio) por mu sub cero y epsilon sub cero ya que trabajamos en el vacío

Luego dejamos expresado en función de la velocidad de la luz y reemplazamos por b = 0,01 metros.

Las unidades de la frecuencia son los hertz (1 sobre segundo) Y 10^9 Hz es un gigahertz entonces

Este modo solo va a propagarse a frecuencias mayores a 15 GHz. Lo que quiere decir, como estamos trabajando exactamente a 15 GHz, que no va a propagarse.

Si el TE 01 no se propago, para ningún valor de n TE 0n va a tener una frecuencia de corte más pequeña, entonces ninguno de los modos con m=0 van a propagarse.

Ahora buscamos que modos con m=1 van a propagarse.

Modo transversal eléctrico 10

El modo TE 10 tiene valores m=1 y n=0. Para ver su frecuencia de corte reemplazamos los valores de m y n en la ecuación de la frecuencia de corte, y a mu y a epsilon (permeabilidad y permitividad del medio) por mu sub cero y epsilon sub cero ya que trabajamos en el vacío y por el valor de a = 0,025 metros

Como la frecuencia de corte es 6 GHz y trabajamos a 15 GHz, este modo va a propagarse.

Modo transversal eléctrico 11

El modo TE 11 tiene valores m=1 y n=1. Para ver su frecuencia de corte reemplazamos los valores de m y n en la ecuación de la frecuencia de corte, y a mu y a epsilon (permeabilidad y permitividad del medio) por mu sub cero y epsilon sub cero ya que trabajamos en el vacío y por los valores de a = 0,025 metros y b = 0,01 metros

La frecuencia de corte es mayor que 15 GHz, luego este modo no se va a propagar.

Con m=1 todos los demás valores de n me van a dar una frecuencia de corte mayor, entonces pruebo con m=2

Modo transversal eléctrico 20

El modo TE 20 tiene valores m=2 y n=0. Para ver su frecuencia de corte reemplazamos los valores de m y n en la ecuación de la frecuencia de corte, y a mu y a epsilon (permeabilidad y permitividad del medio) por mu sub cero y epsilon sub cero ya que trabajamos en el vacío y por los valores de a = 0,025 metros y b = 0,01 metros

Esta frecuencia de corte (12 Hz) es menor a 15 Hz entonces este modo va a propagarse.

Modo transversal eléctrico 21

De la misma manera que antes

La frecuencia de corte de este modo es 19,2.. GHz y es mayor a 15 Hz, entonces este modo no va a propagarse tampoco.

Pruebo con m=3

Modo transversal eléctrico 30

De la misma manera que antes

La frecuencia de corte de este modo es 18 GHz, este modo no va a propagarse tampoco.

Entonces con m=3 ningún valor de n me va a dar una frecuencia menor a 15 GHz.

Y si con m=3 obtengo 19,2.. GHz, para valores mayores de m solo puedo obtener una frecuencia de corte mayor, entonces ya analice todos los modos que pueden propagarse en la guía.

Luego, los modos que se propagan en la guía son TE 10 y TE 20.

Frecuencia de corte a partir de la cual un modo se propaga en una guía

La constante de propagación gamma para una guía puede calcularse de la siguiente manera

Alfa, su parte real, es la constante de atenuación, y beta, su parte imaginaria es la constante de fase. Un modo solo va a propagarse si beta es distinto de cero, es decir si la constante de propagación es compleja.

Entonces, para que el modo se propague es necesario que el término negativo sea mayor al positivo, es decir que

Se define como frecuencia de corte Wc, a la frecuencia a partir de la cual el modo se propaga, es decir

La frecuencia w es dos pi veces la frecuencia f, entonces la frecuencia de corte Fc es

El pi que esta fuera se cancela con los de la raíz, entonces

¿Qué son los modos?

Los modos son las maneras en que se propaga la energía dentro de la guía.